Página 36 -
1) Como o ícone da apostila sugere, as questões devem ser resolvidas no caderno com cálculos e comentários que fundamentem matematicamente a opção V ou F.
Segue exemplo da resolução da letra
d) Inserindo 9 meios geométricos entre x e y, obtém-se um PG de razão 1/2. assim x/y = 1 024
Lembre-se que inserir n's meios geométricos numa sequência, significa colocar n's termos entre seus extremos, de tal modo que ao 11 meios geométricos por exemplo, formamos uma sequência com 11 termos, como é o caso da questão em tela, vejamos:
X, __, ___, ___, ___, ___, ___, ___, ___, ___, y
a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11
Como vemos, obtivemos uma PG com 11 termos, da qual, conhecemos a1 = x , an=y, n= 11 e q = 1/2, o que é bastante para aplicarmos a fórmula do termo geral e garantirmos a veracidade da afirmação.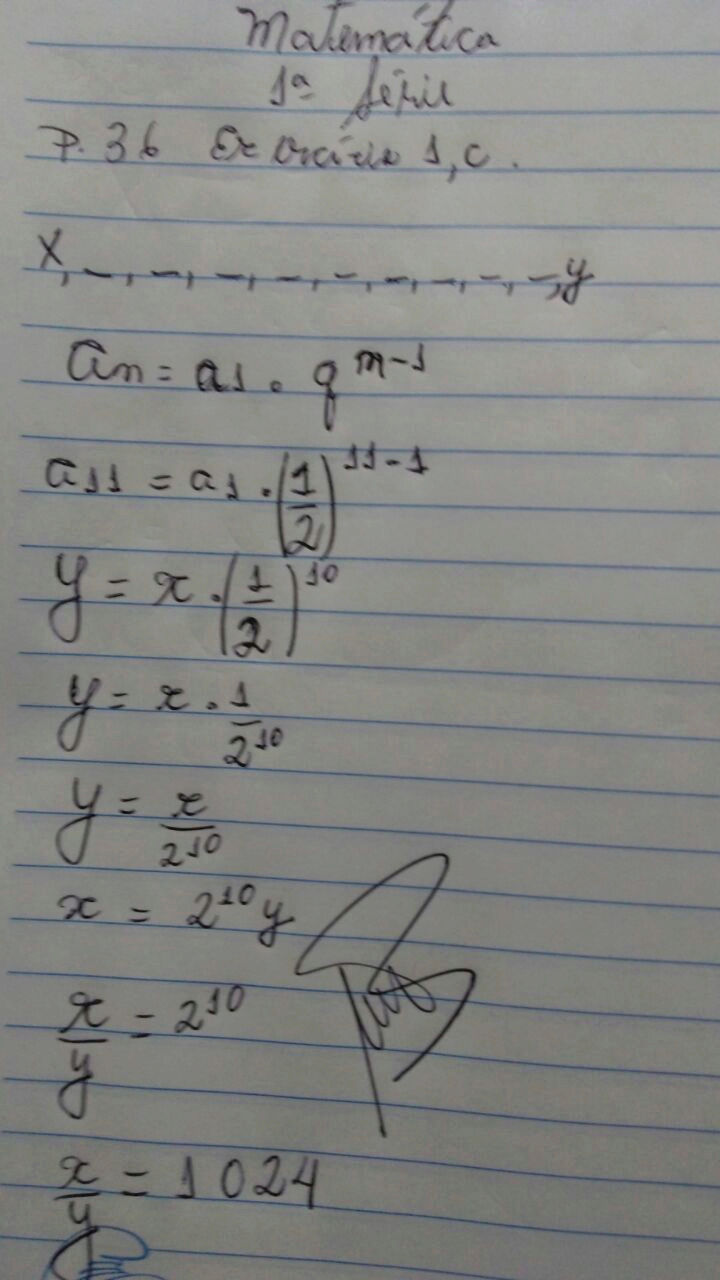
Exercício 2 p. 36
O Desafio consiste em somar as quantidades de casos da gripe suína no período de 2010 a 2015. Para isso há pelo menos dois caminhos possíveis. O primeiro é descobrir a quantidade de casos ano a ano e depois somar e o segundo é aplicar a equação da soma dos termos da PG e fazer esse cálculo de forma direta sem precisar descobrir as quantidades intermediárias de casos. Vamos resolver pelos dois processos.
Caminho I

Caminho II

1) Como o ícone da apostila sugere, as questões devem ser resolvidas no caderno com cálculos e comentários que fundamentem matematicamente a opção V ou F.
Segue exemplo da resolução da letra
d) Inserindo 9 meios geométricos entre x e y, obtém-se um PG de razão 1/2. assim x/y = 1 024
Lembre-se que inserir n's meios geométricos numa sequência, significa colocar n's termos entre seus extremos, de tal modo que ao 11 meios geométricos por exemplo, formamos uma sequência com 11 termos, como é o caso da questão em tela, vejamos:
X, __, ___, ___, ___, ___, ___, ___, ___, ___, y
a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11
Como vemos, obtivemos uma PG com 11 termos, da qual, conhecemos a1 = x , an=y, n= 11 e q = 1/2, o que é bastante para aplicarmos a fórmula do termo geral e garantirmos a veracidade da afirmação.
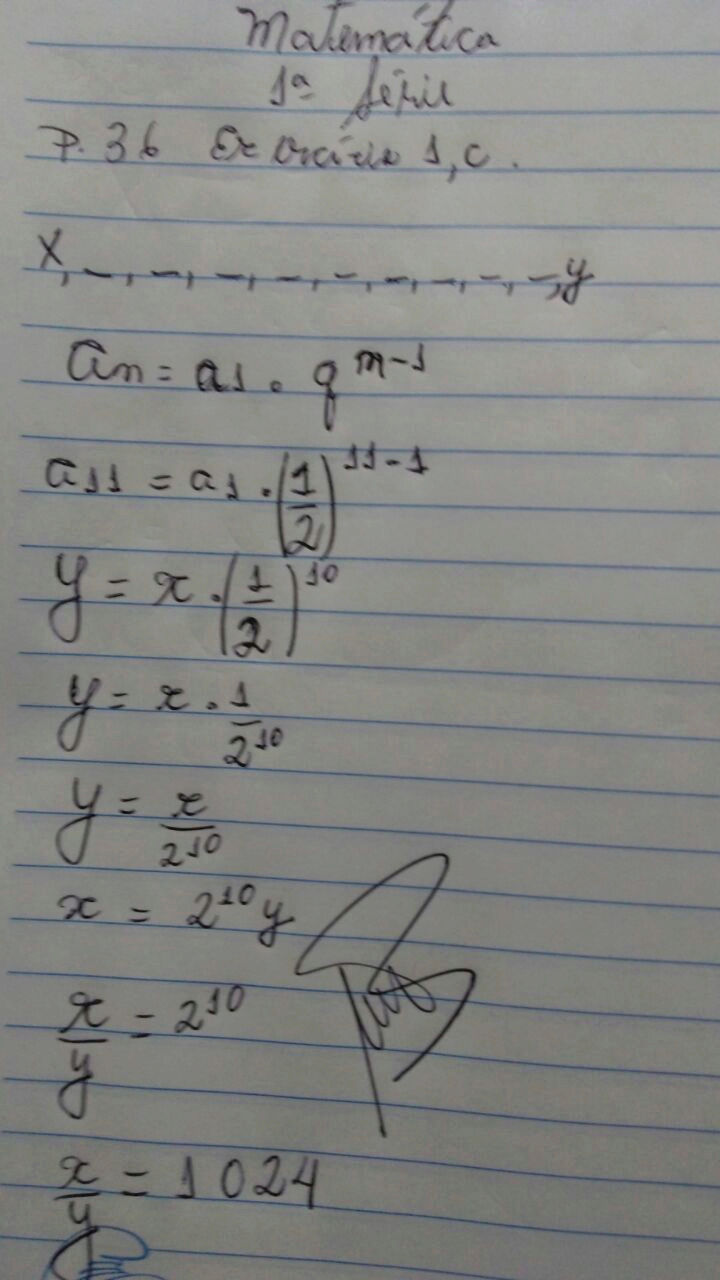
Exercício 2 p. 36
O Desafio consiste em somar as quantidades de casos da gripe suína no período de 2010 a 2015. Para isso há pelo menos dois caminhos possíveis. O primeiro é descobrir a quantidade de casos ano a ano e depois somar e o segundo é aplicar a equação da soma dos termos da PG e fazer esse cálculo de forma direta sem precisar descobrir as quantidades intermediárias de casos. Vamos resolver pelos dois processos.
Caminho I

Caminho II


 Início
Início